Example 3 : Cubic
We test the example whose energy function is shown by \begin{aligned} E(x)=\sum_{j=1}^{n}j(x_{j}^{2}-1)^{2}. \end{aligned}
In particular,we take $n=3$.It is obvious that there are 27 saddle points \((a,b,c),a,b,c \in \{-1,0,1\}\) who happen to be the vertices, face centers, and body center of a cube.
First, we add the path of the saddlescape-1.0 directory to the system path.
import sys
import os
sys.path.append(os.path.abspath(os.path.join(os.getcwd(), '..', 'saddlescape-1.0')))
Then, we import the main class.
from saddlescape import Landscape
import numpy as np
# import packages needed
We define the energy function in 3-D.
energyfunction=""
for i in range(3):
energyfunction+=str(i+1)+"*(x"+str(i+1)+"**2-1)**2+"
energyfunction=energyfunction[:-1]
We initialize the solver and run it.
# parameter initialization
x0 = np.array([0 for i in range(3)]) # initial point
dt = 1e-3 # time step
k = 3 # the maximum index of saddle point
acceme = 'nesterov'
neschoice = 2
nesres = 100
mom = 0.8
maxiter = 1000 # max iter
MyLandscape = Landscape(MaxIndex=k, AutoDiff=True, EnergyFunction=energyfunction, InitialPoint=x0,
TimeStep=dt, Acceleration=acceme, EigenCombination='all',
EigenMethod='euler', BBStep=False, NesterovChoice=neschoice, NesterovRestart=nesres,
Momentum=mom, MaxIter=maxiter, Verbose=True, ReportInterval=100,
EigenMaxIter=10, PerturbationRadius=1e-2)
# Instantiation
MyLandscape.Run()
# Calculate
HiSD Solver Configuration:
------------------------------
[HiSD] Current parameters (initialized):
[Config Sync] `Dim` parameter auto-adjusted to 3 based on `InitialPoint` dimensionality.
Parameter `NumericalGrad` not specified - using default value False.
Parameter `DimerLength` not specified - using default value 1e-05.
Parameter `Tolerance` not specified - using default value 1e-06.
Parameter `SearchArea` not specified - using default value 1000.0.
Parameter `HessianDimerLength` not specified - using default value 1e-05.
Parameter `EigenStepSize` not specified - using default value 1e-05.
Parameter `ExactHessian` not specified - using default value False.
Parameter `PrecisionTol` not specified - using default value 1e-05.
Parameter `EigvecUnified` not specified - using default value False.
Parameter 'GradientSystem' not provided. Enabling automatic symmetry detection.
Parameter 'SymmetryCheck' not provided. Defaulting to True with automatic detection if available.
Gradient system detected. Activating HiSD algorithm.
Landscape Configuration:
------------------------------
[Landscape] Current parameters (initialized):
Parameter `SameJudgementMethod` not specified - using default value <function LandscapeCheckParam.<locals>.<lambda> at 0x000002D073C50D30>.
Parameter `PerturbationMethod` not specified - using default value uniform.
Parameter `InitialEigenVectors` not specified - using default value None.
Parameter `PerturbationNumber` not specified - using default value 2.
Parameter `SaveTrajectory` not specified - using default value True.
Parameter `MaxIndexGap` not specified - using default value 1.
Start running:
------------------------------
From initial point search index-3:
------------------------------
Iteration: 100|| Norm of gradient: 0.000395
Iteration: 200|| Norm of gradient: 0.000011
Non-degenerate saddle point identified: Morse index =3 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 0.701095
Iteration: 200|| Norm of gradient: 0.120058
Iteration: 300|| Norm of gradient: 0.002034
Iteration: 400|| Norm of gradient: 0.000060
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 0.701121
Iteration: 200|| Norm of gradient: 0.120000
Iteration: 300|| Norm of gradient: 0.002032
Iteration: 400|| Norm of gradient: 0.000059
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 0.877872
Iteration: 200|| Norm of gradient: 0.157527
Iteration: 300|| Norm of gradient: 0.006545
Iteration: 400|| Norm of gradient: 0.000194
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 0.877896
Iteration: 200|| Norm of gradient: 0.157552
Iteration: 300|| Norm of gradient: 0.006546
Iteration: 400|| Norm of gradient: 0.000194
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 3.268317
Iteration: 200|| Norm of gradient: 0.001273
Iteration: 300|| Norm of gradient: 0.000014
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 3.268640
Iteration: 200|| Norm of gradient: 0.001272
Iteration: 300|| Norm of gradient: 0.000014
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 2.725669
Iteration: 200|| Norm of gradient: 0.289363
Iteration: 300|| Norm of gradient: 0.000828
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 2.725944
Iteration: 200|| Norm of gradient: 0.289275
Iteration: 300|| Norm of gradient: 0.000828
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 2.721569
Iteration: 200|| Norm of gradient: 0.019025
Iteration: 300|| Norm of gradient: 0.000049
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 2.721581
Iteration: 200|| Norm of gradient: 0.019025
Iteration: 300|| Norm of gradient: 0.000049
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 2.739767
Iteration: 200|| Norm of gradient: 0.018057
Iteration: 300|| Norm of gradient: 0.000046
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-3, ID-0) search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 2.739761
Iteration: 200|| Norm of gradient: 0.018057
Iteration: 300|| Norm of gradient: 0.000046
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-2, ID-1) search index-1:
------------------------------
Iteration: 100|| Norm of gradient: 4.902430
Iteration: 200|| Norm of gradient: 0.001221
Iteration: 300|| Norm of gradient: 0.000026
Non-degenerate saddle point identified: Morse index =1 (number of negative eigenvalues).
……(For the complete results, please refer to the file in the GitHub repository)
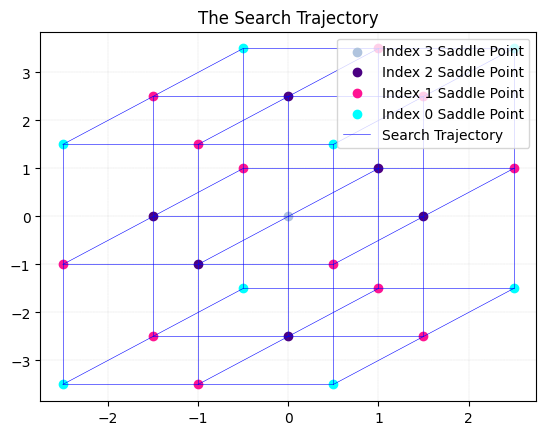
Because the system is 3-D, we define a projection function to draw the trajectory.
def proj_func(input):
output = np.hstack((1.0 * input[:, [0]]+ 1.5 * input[:, [1]], 1.0 * input[:, [0]]+ 2.5 * input[:, [2]]))
return output
MyLandscape.DrawTrajectory(ContourGridNum=100, ContourGridOut=25, Projection=proj_func)
# Draw the search path. But because of the large dimension, we cannot draw the picture.
[WARNING] Contour plot and heatmap cannot be generated after projection because the projection function may not be injective.
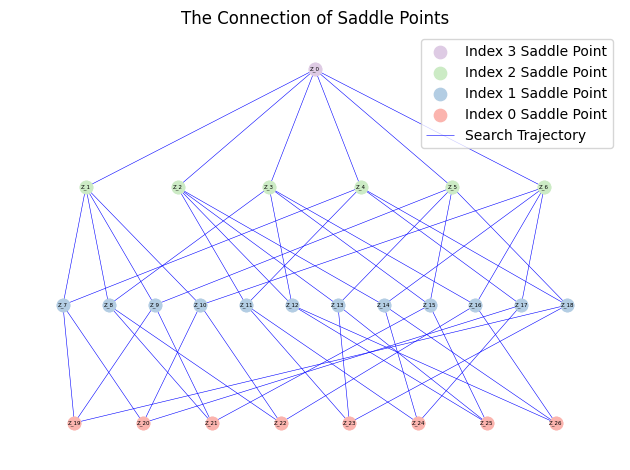
We can also draw the solution landscape and save the data.
MyLandscape.DrawConnection()
MyLandscape.Save('output/Ex_Cubic','mat')
# Save the data