示例1:蝴蝶
我们测试一个热图类似于蝴蝶形状的示例,其能量函数如下所示:
\[\begin{aligned} E(x,y)=x^{4}-1.5x^{2}y^{2}+y^{4}-2y^{3}+y^{2}+x^{2}y-2x^{2}. \end{aligned}\]首先,我们将 saddlescape-1.0 目录的路径添加到系统路径中:
import sys
import os
sys.path.append(os.path.abspath(os.path.join(os.getcwd(), '..', 'saddlescape-1.0')))
接着,我们导入主类:
from saddlescape import Landscape
import numpy as np
# import packages needed
定义能量函数:
energyfunction = 'x1**4 -1.5*x1**2*x2**2+ x2**4 - 2*x2**3 + x2**2 + x1**2*x2 - 2*x1**2'
# given energy function
# parameter initialization
x0 = np.array([0.1, 0.1]) # initial point
dt = 1e-2 # time step
k = 2 # the maximum index of saddle point
acceme = 'none'
maxiter = 10000 # max iter
初始化求解器并运行它:
MyLandscape = Landscape(MaxIndex=k, AutoDiff=True, EnergyFunction=energyfunction,
EigenMethod='euler', EigenMaxIter=1, InitialPoint=x0,
TimeStep=dt, Acceleration=acceme, MaxIter=maxiter,
EigenCombination='all', PerturbationNumber=1,
PerturbationRadius=1e-2, Verbose=True, ReportInterval=100)
# Instantiation
MyLandscape.Run()
HiSD Solver Configuration:
------------------------------
[HiSD] Current parameters (initialized):
[Config Sync] `Dim` parameter auto-adjusted to 2 based on `InitialPoint` dimensionality.
Parameter `NumericalGrad` not specified - using default value False.
Parameter `Momentum` not specified - using default value 0.0.
Parameter `BBStep` not specified - using default value False.
Parameter `DimerLength` not specified - using default value 1e-05.
Parameter `Tolerance` not specified - using default value 1e-06.
Parameter `NesterovChoice` not specified - using default value 1.
Parameter `SearchArea` not specified - using default value 1000.0.
Parameter `NesterovRestart` not specified - using default value None.
Parameter `HessianDimerLength` not specified - using default value 1e-05.
Parameter `EigenStepSize` not specified - using default value 1e-05.
Parameter `ExactHessian` not specified - using default value False.
Parameter `PrecisionTol` not specified - using default value 1e-05.
Parameter `EigvecUnified` not specified - using default value False.
Parameter 'GradientSystem' not provided. Enabling automatic symmetry detection.
Parameter 'SymmetryCheck' not provided. Defaulting to True with automatic detection if available.
Gradient system detected. Activating HiSD algorithm.
Landscape Configuration:
------------------------------
[Landscape] Current parameters (initialized):
Parameter `SameJudgementMethod` not specified - using default value <function LandscapeCheckParam.<locals>.<lambda> at 0x000002CD1746C670>.
Parameter `PerturbationMethod` not specified - using default value uniform.
Parameter `InitialEigenVectors` not specified - using default value None.
Parameter `SaveTrajectory` not specified - using default value True.
Parameter `MaxIndexGap` not specified - using default value 1.
Start running:
------------------------------
From initial point search index-2:
------------------------------
Iteration: 100|| Norm of gradient: 0.176823
Iteration: 200|| Norm of gradient: 0.084819
Iteration: 300|| Norm of gradient: 0.032330
Iteration: 400|| Norm of gradient: 0.011899
Iteration: 500|| Norm of gradient: 0.004359
Iteration: 600|| Norm of gradient: 0.001596
Iteration: 700|| Norm of gradient: 0.000584
Iteration: 800|| Norm of gradient: 0.000214
Iteration: 900|| Norm of gradient: 0.000078
Iteration: 1000|| Norm of gradient: 0.000029
Iteration: 1100|| Norm of gradient: 0.000010
Iteration: 1200|| Norm of gradient: 0.000004
Iteration: 1300|| Norm of gradient: 0.000001
Non-degenerate saddle point identified: Morse index =2 (number of negative eigenvalues).
From saddle point (index-2, ID-0) search index-1:
------------------------------
Iteration: 100|| Norm of gradient: 0.023111
Iteration: 200|| Norm of gradient: 0.061258
Iteration: 300|| Norm of gradient: 0.144118
Iteration: 400|| Norm of gradient: 0.183221
Iteration: 500|| Norm of gradient: 0.063280
Iteration: 600|| Norm of gradient: 0.010152
Iteration: 700|| Norm of gradient: 0.001384
Iteration: 800|| Norm of gradient: 0.000184
Iteration: 900|| Norm of gradient: 0.000024
Iteration: 1000|| Norm of gradient: 0.000003
Non-degenerate saddle point identified: Morse index =1 (number of negative eigenvalues).
From saddle point (index-2, ID-0) search index-1:
------------------------------
Iteration: 100|| Norm of gradient: 0.023108
Iteration: 200|| Norm of gradient: 0.061250
Iteration: 300|| Norm of gradient: 0.144105
Iteration: 400|| Norm of gradient: 0.183230
Iteration: 500|| Norm of gradient: 0.063294
Iteration: 600|| Norm of gradient: 0.010155
Iteration: 700|| Norm of gradient: 0.001384
Iteration: 800|| Norm of gradient: 0.000184
Iteration: 900|| Norm of gradient: 0.000024
Iteration: 1000|| Norm of gradient: 0.000003
Non-degenerate saddle point identified: Morse index =1 (number of negative eigenvalues).
From saddle point (index-2, ID-0) search index-1:
------------------------------
Iteration: 100|| Norm of gradient: 0.069550
Iteration: 200|| Norm of gradient: 1.384067
Iteration: 300|| Norm of gradient: 0.016423
Iteration: 400|| Norm of gradient: 0.000428
Iteration: 500|| Norm of gradient: 0.000011
Non-degenerate saddle point identified: Morse index =1 (number of negative eigenvalues).
From saddle point (index-2, ID-0) search index-1:
------------------------------
Iteration: 100|| Norm of gradient: 0.070554
Iteration: 200|| Norm of gradient: 1.382590
Iteration: 300|| Norm of gradient: 0.016414
Iteration: 400|| Norm of gradient: 0.000428
Iteration: 500|| Norm of gradient: 0.000011
Non-degenerate saddle point identified: Morse index =1 (number of negative eigenvalues).
From saddle point (index-1, ID-1) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 2.798815
Iteration: 200|| Norm of gradient: 0.084903
Iteration: 300|| Norm of gradient: 0.000135
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
From saddle point (index-1, ID-1) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 2.798815
Iteration: 200|| Norm of gradient: 0.084903
Iteration: 300|| Norm of gradient: 0.000135
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
From saddle point (index-1, ID-2) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 1.475986
Iteration: 200|| Norm of gradient: 0.295764
Iteration: 300|| Norm of gradient: 0.008081
Iteration: 400|| Norm of gradient: 0.000190
Iteration: 500|| Norm of gradient: 0.000004
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
From saddle point (index-1, ID-2) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 1.475986
Iteration: 200|| Norm of gradient: 0.295764
Iteration: 300|| Norm of gradient: 0.008081
Iteration: 400|| Norm of gradient: 0.000190
Iteration: 500|| Norm of gradient: 0.000004
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
From saddle point (index-1, ID-3) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 1.432133
Iteration: 200|| Norm of gradient: 0.273676
Iteration: 300|| Norm of gradient: 0.000454
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
From saddle point (index-1, ID-3) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 0.818020
Iteration: 200|| Norm of gradient: 0.214057
Iteration: 300|| Norm of gradient: 0.005585
Iteration: 400|| Norm of gradient: 0.000131
Iteration: 500|| Norm of gradient: 0.000003
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
From saddle point (index-1, ID-4) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 0.818020
Iteration: 200|| Norm of gradient: 0.214057
Iteration: 300|| Norm of gradient: 0.005585
Iteration: 400|| Norm of gradient: 0.000131
Iteration: 500|| Norm of gradient: 0.000003
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
From saddle point (index-1, ID-4) search index-0:
------------------------------
Iteration: 100|| Norm of gradient: 1.432133
Iteration: 200|| Norm of gradient: 0.273676
Iteration: 300|| Norm of gradient: 0.000454
Non-degenerate saddle point identified: Morse index =0 (number of negative eigenvalues).
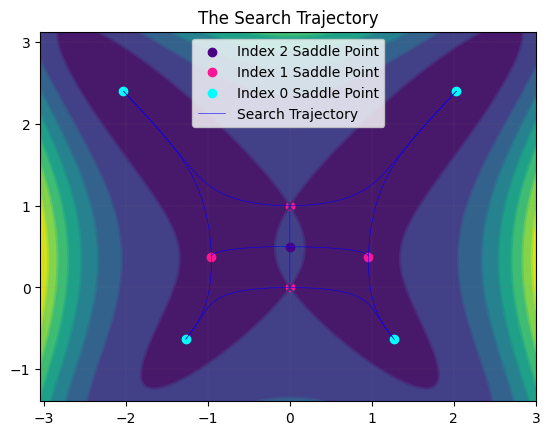
我们可以绘制搜索轨迹。
MyLandscape.DrawTrajectory(ContourGridNum=100, ContourGridOut=25, DetailedTraj=True)
# Draw the search path.
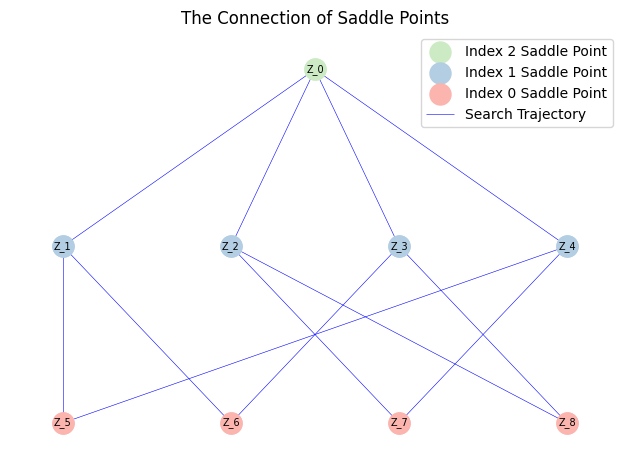
我们也可以绘制解景观并保存数据。
MyLandscape.DrawConnection()
MyLandscape.Save('output/Ex_Butterfly')
# Save the data
然后,我们保存搜索轨迹。
import json
detail = MyLandscape.DetailRecord
output = {
"Start ID": [row[1] for row in detail],
"End ID": [row[0] for row in detail],
"Path Positions": [row[2].tolist() for row in detail],
"Path Times": [row[3].tolist() for row in detail]
}
with open('output/Ex_ButterflyDetail.json', 'w') as f:
json.dump(output, f)
此外,我们可以使用输出数据进行更多的后处理。我们将以生成搜索轨迹的运动图为例。
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import Colormap
def animateSL(fig: plt.Figure,
ax: plt.Axes,
saddleinfo: dict,
trajinfo: dict,
ColorsMI: Colormap = plt.get_cmap("tab10"),
ColorTraj: list|str = "blue",
dt_per_frame: float = 0.2,
fps: int = None):
IDs: list[int] = saddleinfo["IDs"] # Tags of saddles
coords: list[np.ndarray] = saddleinfo["coords"] # Coordinates
MIs: list[int] = saddleinfo["MIs"] # Morse indices
parentIDs: list[list[int]] = saddleinfo["parentIDs"] # Parent saddles
trajectories: list[np.ndarray] = trajinfo["trajectories"] # Trajectories
times: list[np.ndarray] = trajinfo["times"] # times
startIDs: list[int] = trajinfo["startIDs"] # Starting saddle"s tag
endIDs: list[int] = trajinfo["endIDs"] # Ending saddle"s tag
N_traj = len(trajectories) # Number of trajectories
assert N_traj == len(times) == len(startIDs) == len(endIDs)
for i, traj, time in zip(range(N_traj), trajectories, times):
assert len(traj) == len(time), f"Different length of {i}-th trajectory and time"
trajectoriesFrom: list[list[int]] = [[] for _ in range(len(IDs))]
for i, startID in enumerate(startIDs):
if startID >= 0:
trajectoriesFrom[startID].append(i)
colorSaddle: list[tuple] = [ColorsMI(MI) for MI in MIs]
if isinstance(ColorTraj, str):
colorTraj: list[str] = [ColorTraj] * N_traj
ZORDER_TRAJ = 100000
ZORDER_SADDLE = 200000
ZORDER_TEXT = 300000
if fps is None:
fps = 1 / dt_per_frame
lentraj = [len(traj) for traj in trajectories]
saddleArtists = [ax.plot([], [], "o", color=colorSaddle[i], zorder=ZORDER_SADDLE)[0] for i in range(len(IDs))]
trajArtists = [ax.plot([], [], color=colorTraj[i], zorder=ZORDER_TRAJ)[0] for i in range(N_traj)]
startArtists = [ax.plot([], [], color=colorTraj[i], zorder=ZORDER_TRAJ, linestyle="--")[0] for i in range(N_traj)]
endArtists = [ax.plot([], [], color=colorTraj[i], zorder=ZORDER_TRAJ, linestyle="--")[0] for i in range(N_traj)]
_awakeMoment = np.ones(len(IDs)) * np.inf # Activation moment of each saddle
_pendingTraj = []
plotSaddle = lambda id: saddleArtists[id].set_data([coords[id][0]], [coords[id][1]])
startTraj = lambda i: startArtists[i].set_data([coords[startIDs[i]][0], trajectories[i][0, 0]],
[coords[startIDs[i]][1], trajectories[i][0, 1]])
endTraj = lambda i: endArtists[i].set_data([trajectories[i][-1, 0], coords[endIDs[i]][0]],
[trajectories[i][-1, 1], coords[endIDs[i]][1]])
def init_frame():
nonlocal _awakeMoment, _pendingTraj
for id, parentID in enumerate(parentIDs):
if -1 in parentID:
plotSaddle(id)
_awakeMoment[id] = 0.0
for i in trajectoriesFrom[id]:
startTraj(i)
_pendingTraj.append(i)
return saddleArtists + trajArtists + startArtists + endArtists
def frame_generator():
nonlocal _awakeMoment, _pendingTraj
pointer = np.zeros(N_traj, dtype=int)
_pendingSaddle = []
_pendingTraj_temp = []
current_time = 0.0
while _pendingTraj:
current_time += dt_per_frame
while _pendingTraj or _pendingSaddle:
if _pendingTraj:
i = _pendingTraj.pop(0)
startID = startIDs[i]
while pointer[i] < lentraj[i] and times[i][pointer[i]] + _awakeMoment[startID] <= current_time:
pointer[i] += 1
trajArtists[i].set_data(trajectories[i][:pointer[i], 0], trajectories[i][:pointer[i], 1])
if pointer[i] == lentraj[i]:
endTraj(i)
endID = endIDs[i]
if not endID in _pendingSaddle:
_pendingSaddle.append(endID)
if _awakeMoment[endID] > times[i][-1] + _awakeMoment[startID]:
_awakeMoment[endID] = times[i][-1] + _awakeMoment[startID]
_pendingSaddle.sort(key=lambda id: _awakeMoment[id])
else:
_pendingTraj_temp.append(i)
else:
id = _pendingSaddle.pop(0)
plotSaddle(id)
_pendingTraj += trajectoriesFrom[id]
yield saddleArtists + trajArtists + startArtists + endArtists
_pendingTraj = _pendingTraj_temp.copy()
_pendingTraj_temp.clear()
return FuncAnimation(fig,
lambda frame: frame,
frame_generator,
init_frame,
blit=True,
interval=dt_per_frame * 1000,
cache_frame_data=False)
import json
dpi: float = 100
xlim = [-3, 3]
ylim = [-2, 3]
fig, ax = plt.subplots(dpi=dpi)
ax.set_xlim(xlim)
ax.set_ylim(ylim)
ax.set_aspect("equal")
x, y = np.meshgrid(np.linspace(xlim[0], xlim[1], 100), np.linspace(ylim[0], ylim[1], 100))
z = x**4 - 1.5*x**2*y**2 + y**4 - 2*y**3 + y**2 + x**2*y - 2*x**2 # SPECIFIC
contourf_args: dict = {"levels": 20}
if "levels" in contourf_args and contourf_args["levels"] >= 0:
ax.contourf(x, y, z, **contourf_args)
with open("output/Ex_Butterfly.json", "r") as f:
saddle_data = json.load(f) # Load the data
saddleinfo = {"IDs": saddle_data["SaddleID"],
"coords": np.array(saddle_data["Position"])[:, :, 0],
"MIs": saddle_data["MorseIndex"],
"parentIDs": saddle_data["FatherSet"]}
with open("output/Ex_ButterflyDetail.json", "r") as f:
traj_data = json.load(f) # Load the data
trajinfo = {"trajectories": [np.array(traj) for traj in traj_data["Path Positions"]],
"times": [time for time in traj_data["Path Times"]],
"startIDs": traj_data["Start ID"],
"endIDs": traj_data["End ID"]}
ani = animateSL(fig, ax, saddleinfo, trajinfo, dt_per_frame=0.02)
我们可以将动画导出为不同的文件类型。
ani.save("output/Ex_Butterfly.mp4", writer="ffmpeg") # Must install ffmpeg
生成的动画图像显示如下: