背景介绍：构建复杂系统的解景观

很多物理、化学等领域的实际问题都可以被归为求解具有多个变量的非线性函数或泛函的极小值问题，其应用包括材料科学、软物质、凝聚态物理、生命科学、数据科学等领域。作为多解问题的一个共同特征，物理变量的函数或泛函对应的能量景观有很多的极小，每一个极小对应于物理上的一个亚稳态，不同的极小被能量势垒所分隔。这些变量可能是蛋白质折叠中的氨基酸位置，原子簇的原子位置，描述嵌段共聚物自组装的连续场变量，或者神经网络的参数等。

非线性问题的平衡态对应于满足$\nabla E(\boldsymbol{x})=0$方程的驻点(平衡点)。能量景观中的非退化驻点(即驻点处海瑟矩阵没有零特征值)在数学上可以利用Morse理论中的Morse指标进行分类。Morse指标是驻点处海瑟矩阵的最大负定子空间的维数，等价于其海瑟矩阵的负特征值的个数。具体而言，Morse指标为0的驻点对应稳定的极小点;而不稳定的鞍点是Morse指标非0的驻点，例如一个$k$阶鞍点是其海瑟矩阵有$k$个负特征值的驻点。

特别地，1阶鞍点通常被称为过渡态，是位于两个极小值之间势垒最小的点。最小能量路径则是能量景观上连接了两个极小值和过渡态的一条连续曲线。过渡态在很多科学领域中有着非常重要的作用，例如寻找临界核与相变中的转移路径，计算化学反应的转换速率以及生物领域等。

寻找所有的驻点对于理解能量景观至关重要，但由于鞍点的不稳定性，计算不稳定的鞍点通常要比计算稳定的极小点要困难得多。近年来，很多著名的数学家、物理学家、化学家发展了一系列计算稀有事件及1阶鞍点的数值算法，其主要分为两类（如图1）:

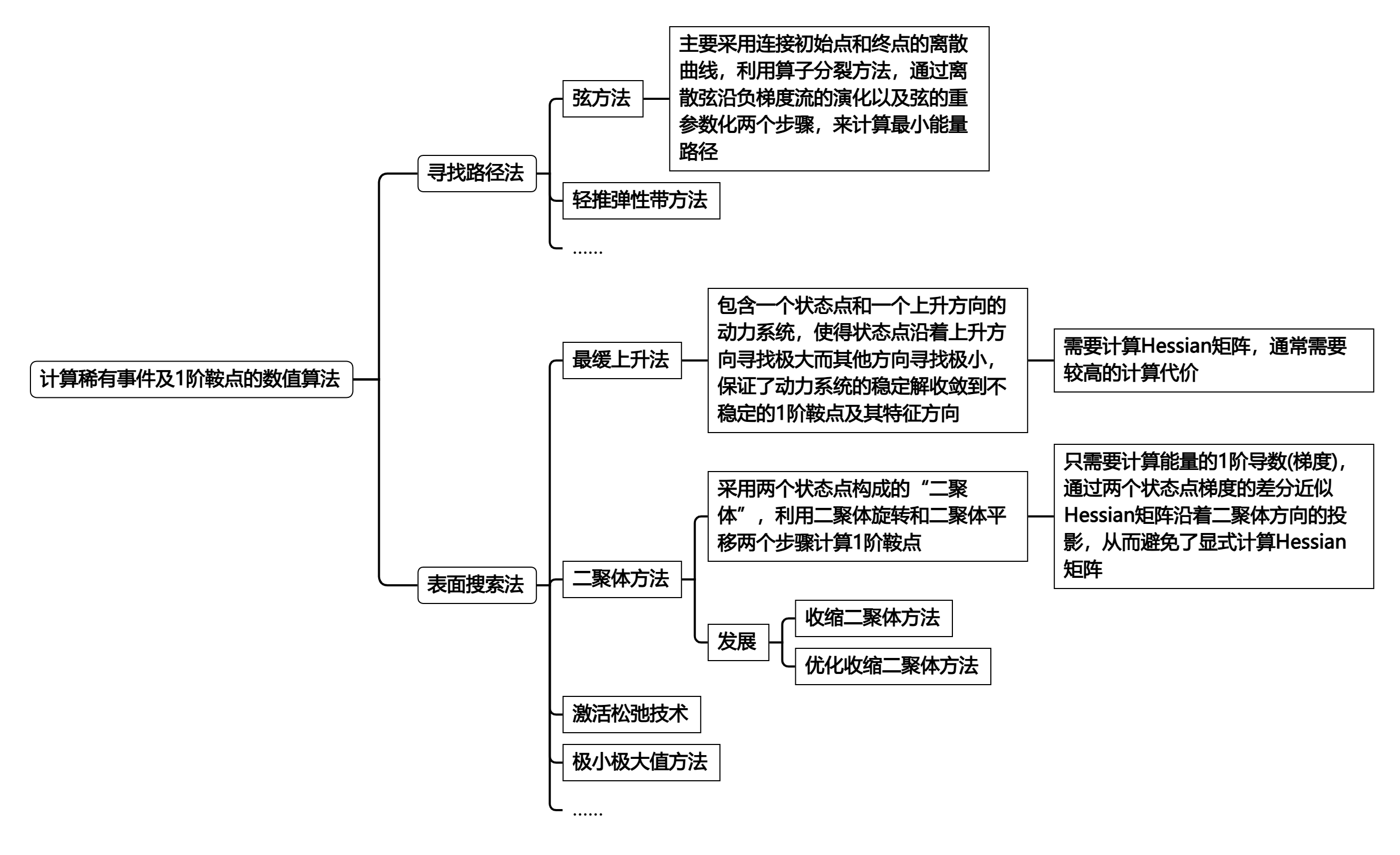
相比于1阶鞍点，针对高阶鞍点计算方法的发展还十分缓慢。一方面是源于高阶鞍点有更多的不稳定方向，致使部分1阶鞍点算法的技术不再适用;另一方面是高阶鞍点在实际问题中的物理意义和作用还不明显，缺乏足够的动力去解决这一问题。实际上，很多研究已指出，非线性问题中高阶鞍点的数量远多于极小点和1阶鞍点。因此，如何寻找复杂系统的全部解和不同解之间的连接关系始终是计算数学领域一个非常重要且具有挑战性的科学问题。

近年来，我们提出了一个”解景观”(solution landscape)的新概念。首先，我们将解景观定义为一个包含所有解和解与解之间连接关系的路径图。这里的解包含了所有稳定的极小解和不稳定的鞍点解，而路径图描述了不同的极小被相应的一阶鞍点连接，低阶鞍点被相应的高阶鞍点连接的层次结构图，如图2。我们可以将解景观直观地比喻成一个家谱，家谱的第一代对应为系统的最高阶鞍点，而家谱的最年轻一代代表系统的极小点。家谱中所有的极小点都不是孤立的，可以从第一代开始，沿着一条路径，连接到每一个极小。

尽管解景观的定义很直观，但数值上计算解景观仍然是非常具有挑战性的。构建解景观的主要困难在于如何高效地计算解景观中的各阶鞍点。现有的求解非线性方程$\nabla E(\boldsymbol{x})=0$的计算方法，包括homotopy方法和deflation技术，能够找到方程的多个平衡解。然而，随着找到越来越多的解，对于剩余平衡解的计算需要精细调节初始猜测，这使得计算越来越困难，并且难以确定是否已找到所有的解。此外，这些方法通常得到的是平衡解的集合，不能揭示不同解的连接关系。为了克服这一难题，我们发展了一个新的鞍点动力学(saddle dynamics)，将计算不稳定的高阶鞍点转换成计算高阶鞍点动力学的稳定解，并通过鞍点动力学给出解景观中不同阶鞍点/极小的连接关系。

参考文献

1. Zhang, L. (2023). Construction of solution landscapes for complex systems. Mathematica Numerica Sinica, ​45(3), 267-283. https://doi.org/10.12286/jssx.j2023-1121